Further Reading
The argument I've made in this video has been outlined quite a few times by Stuart Kauffman (and others) over the decades, but here are some of its clearest instantiations:
Giuseppe Longo
Limitations of the Newtonian paradigm
Marina CortêsMarina Cortês
Contributors to Wikimedia projects
Laws of nature and ceteris paribus laws
Yes I know, the way I defined a scientific law in the video was a bit odd. I presume a lot of philosophers are going to be angry with me on that (especially given the sources below).
But that's why I tried to emphasise that what I was arguing for the non-existence of is laws of biology qua universal/immutable differential equations. Whether there are other laws of biology is a topic for another day.
Nancy Cartwright
John Earman
Perspectival realism and how to do science without laws
Michela Massimi
WILLIAM C. WIMSATT
Sources
Physics envy is the feeling you get when you wish your scientific field was as precise as physics.
It's not hard to see why this is a genuine phenomenon amongst scientists.
Contributors to Wikimedia projects
Biology, psychology and sociology are all incredibly complex and it would be really really nice to find universal laws that could help us to untangle their messiness.
It's exactly how I thought when I made the first video on this channel, that ended with this diagram exploring the role of mathematics in biology and physics.
Both fields have mathematical models for specific situations like pendulums or pandemics. But only physics has the universal laws.
I'm not the only one who's thought like this either. It's often said that evolution has four driving forces: natural selection, mutation, genetic drift and migration.
But 'forces' is really a very odd choice of word for describing how a population evolves statistically over time. I wonder where these biologists got it from.
Then there's one the founders of population genetics, Ronald Fisher, who constructed what he called "The Fundamental Theorem of Natural Selection" which he likened to the second law of thermodynamics saying:
It is not a little instructive that so similar a law should hold the supreme position among the biological sciences.
It turns out that Fisher's theorem, when interpreted correctly, is hardly as significant as he thought it was. Definitely not anything close to as useful as the second law of thermodynamics.
And in a modern context, biologists are keenly aware that there is a lot more going on in evolution than just these four 'forces'.
There's things like niche construction where organisms make their own environments like beaver dams, complex symbiotic interactions like the bacteria that live inside insects, the role of development studied in the field of evo-devo and so on and so forth.
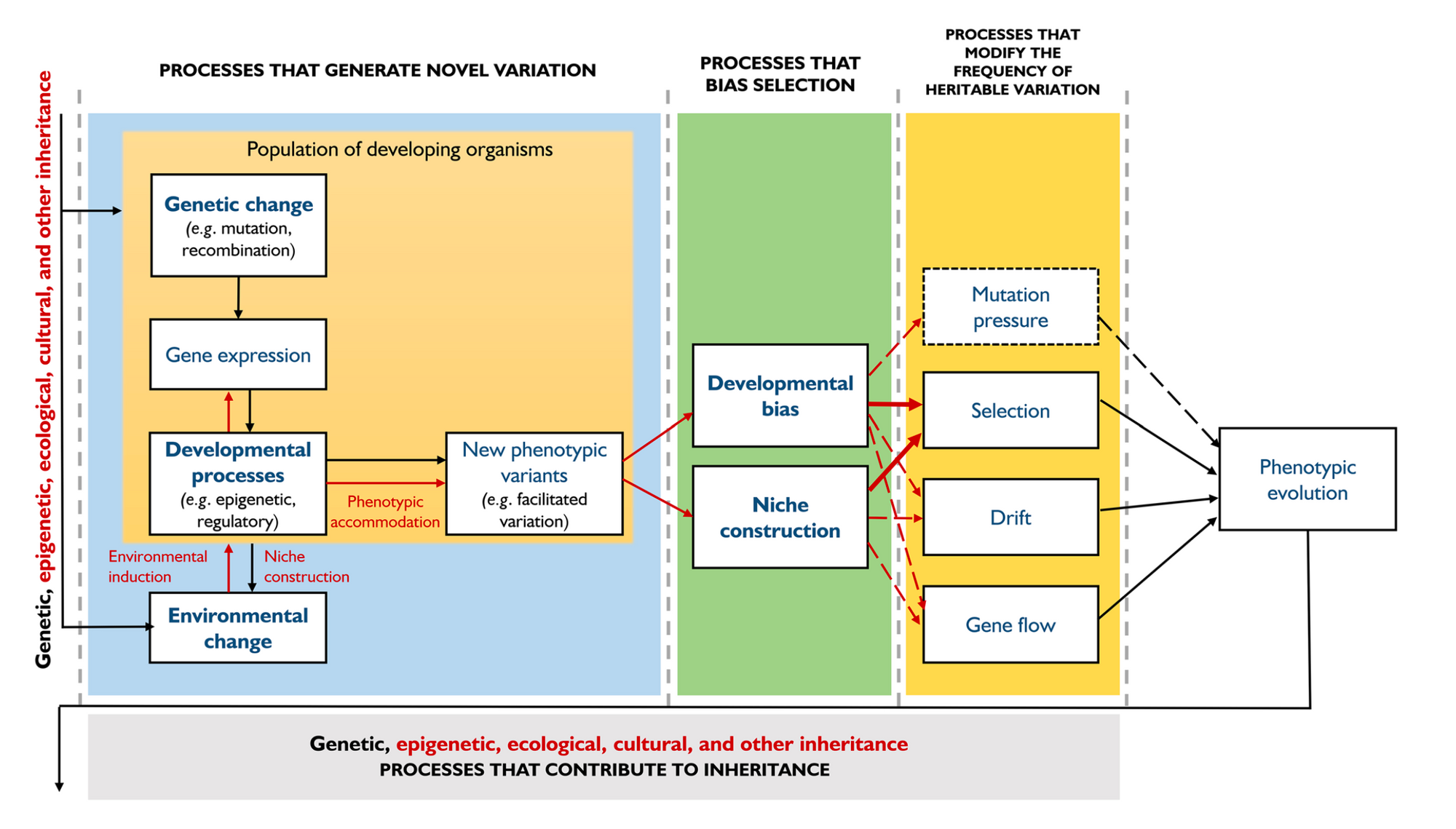
So no attempts to 'Newtonise' biology have really worked.
But that doesn't rule out universal laws in principle, right? They could be out there, we just haven't found them yet, right?
Let's try a thought experiment and think about what a law of biology would look like if it existed.
If we really wanted this law to be one that resembles the most significant laws of physics, it would have to be some kind of a differential equation, or a system of them.
Note: This is perhaps a contentious statement. Are there not many laws of nature that are non-differential equation based (e.g. Noether's theorem)? Are the laws of physics really the DE-based models we construct or are they the more fundamental principles used to construct them?
These are sound interjections which I am actually inclined to agree with. Indeed, there is a lot of philosophical literature arguing over what it means to be a scientific law (see the references linked in the further reading section above.)
But as is the theme in several of my videos, I am just taking one definition that tends to get used a lot (whether or not it is a good one is a separate story) and seeing if it applies to biology.
We could certainly talk about the possibility of non-DE based laws in biology, but I think a similar argument will also work against them. The biosphere is constantly evolving in fundamentally new ways, so any kind of law will have to necessarily evolve too. There will be no 'axioms' or 'universal principles' of biology, DEs or no DEs.
My claim that the more general argument also holds was reason enough to hone in on DEs.
These equations have been the language of physics since Newton. They work by first describing a relatively isolated system - physicists call this finding boundary conditions - and then describing the system's initial state via a set of initial conditions. If you plug all of that into your differential equation, it will tell you exactly what the system will look like at any point from now. Pretty sweet.
This way of doing physics (what Lee Smolin calls the Newtonian paradigm) has remained relatively unchanged throughout the revolutions of the 20th century.
General relativity still works on differential equations, albeit 10 very complicated ones.
And so too does quantum mechanics, but instead of tracking the exact states of the system, the Schrödinger equation tracks the evolution of the system's quantum state, which has some inherent randomness built in.
Moving back to biology, if we wanted to replicate this, we'd need:
1 An differential equation that can model life,
2 A mostly isolated system to study - let's take an individual bacterial cell. And
3 A set of boundary and initial conditions for that system - and let's just say we know what these are.
So all we need now is the differential equation itself.
For a bacterial cell, this equation would have to be monstrously complicated accounting for a whole range of biological processes like: gene expression, protein folding, cell division, food metabolism, DNA repair, enzyme-substrate interactions plus a whole bunch of others.
Overlooking how difficult it would be to model all of these processes perfectly, this model would seem to allow us to predict exactly what a cell will look like at any point from now.
So would this huge hypothetical equation count as a meaningful law of biology?
No. Here's why.
Whenever we use a differential equation to model a particular system, we automatically construct a corresponding phase space for the system. This is the range of possible states that a system could take.
For instance, in this model of a simple pendulum, the phase space would be all the possible velocities of the pendulum together with all its possible positions as it spins around.
Contributors to Wikimedia projects
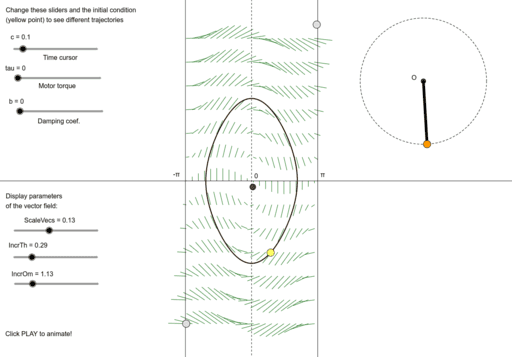
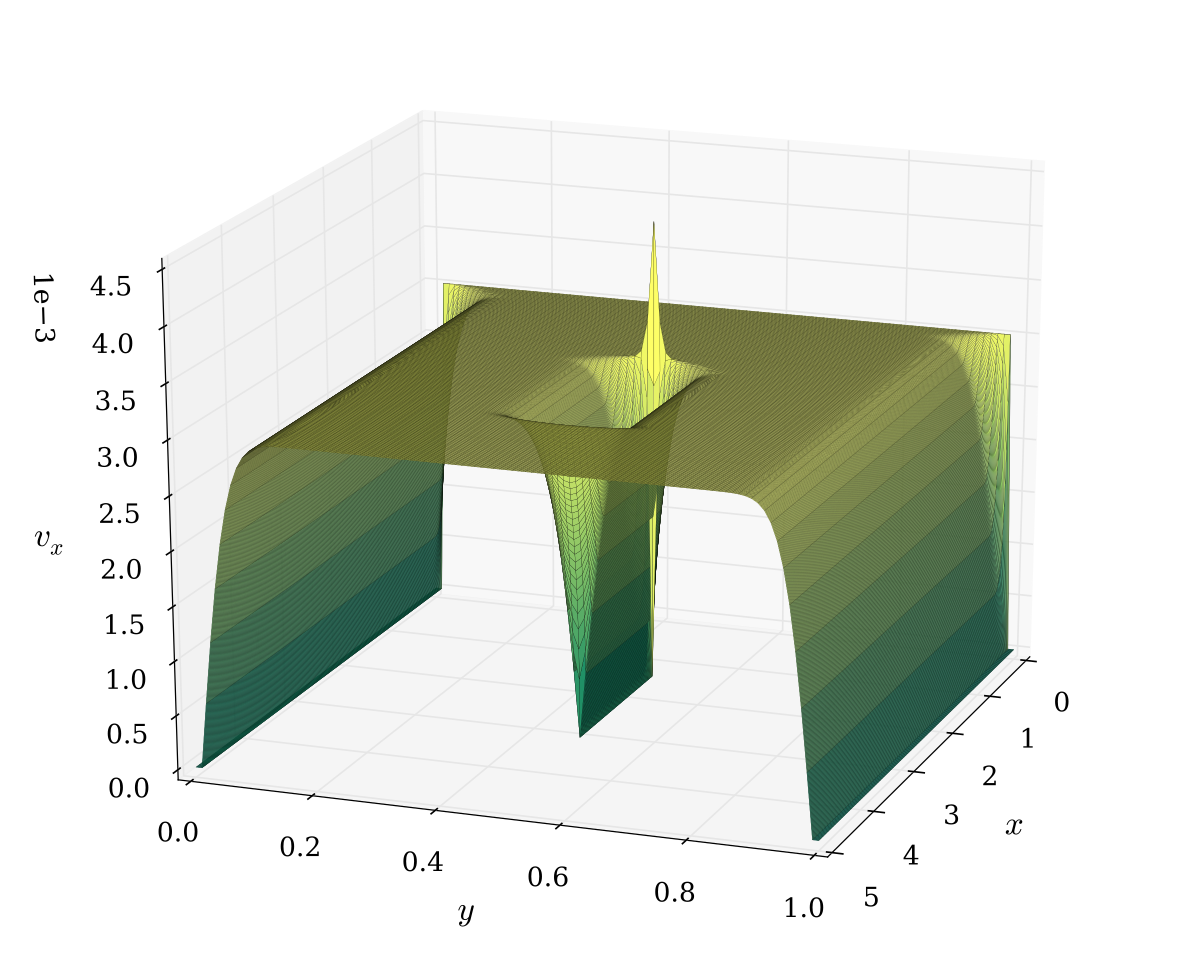
In the case of our model of the cell, we'll also get a phase space containing all the possible states of our little bacterium.
That will involve: all the possible proteins that could exist in the cell at any one time, together with how many of them there are, plus how fast they're going and their position and the same for every other relevant molecule.
It's going to be a stupidly big phase space, with a huge number of dimensions, but by the way differential equations work, it will still be well-defined.
Now here comes the problem.
Biological organisms are very much not isolated systems. Remember, that's one of the features you need for a model based on differential equations to work properly.
This is really one of the key differences between physics and biology. In physics, isolated systems are created and studied all the time.
But biological organisms can never be completely isolated from their environments. They'll always be searching for new food sources, interacting with different species, and just doing new unexpected things.
Of course, we can approximately isolate organisms inside labs - like I did here by putting fruit flies into test tubes - but that's very far from what fruit flies are genuinely like in the wild.
Ok so why does that matter?
Well, the problem is that we know that new ecological interactions can have a fundamental impact on biological evolution.
For example, at some point along the way, biologists are pretty sure that one bacteria came to live inside another living cell. And this relationship eventually become so crucial that the little bacterium evolved into mitochondria - yes, the powerhouse of the cell.
Contributors to Wikimedia projects
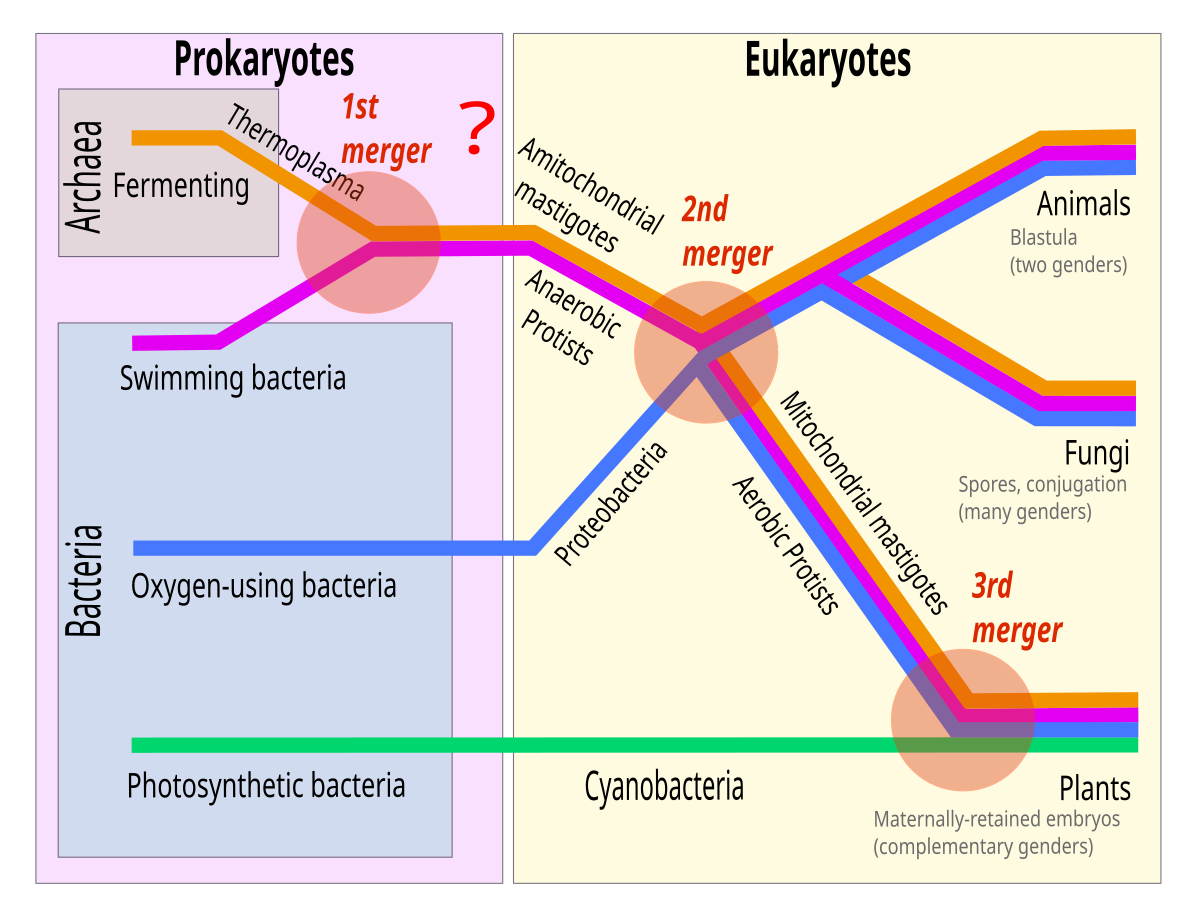
But this possibility wasn't in our original model since it only tracked the processes happening inside the cell, plus maybe some background environmental interactions.
We certainly didn't account for the case of the bacterium being engulfed by a cell, accidentally not being digested, and kept alive over many generations to the point that it came to lose most of its original functions and became specialised in energy production.
This just wasn't in the phase space of our model.
Ok so our initial model was incomplete. For the reductionist, that doesn't seem to be a huge threat, we can just make the model bigger. That means tracking every other cell on the planet, plus how much energy they produce, what their membranes look like and every other little detail.
But even then, we'd also have to realise that this bacterium we're studying could also just as easily move into the digestive tract of a fish, and make a home for itself there in a very new environment with brand new boundary conditions. And it could do this for any animal on earth.
Those possibilities weren't in our phase space either, so we'd need to add all of them in too.
And then maybe a cosmic ray comes from a distant galaxy to smash into the DNA of our cell, causing a new kind of mutation, that unlocks a brand new path of evolution that we hadn't considered in our model.
So we also need to add those galaxies into our model. And this process goes on and on as our organism continues to do new things and experience new changes.
One of the world's leading theoretical biologists, Stuart Kauffman, calls this concept the "ever-expanding configuration space" of the organism.
And this idea has been physicist-approved in an amazing paper published just last year co-written with Marina Cortes, Andrew Liddle and Lee Smolin.
Just by virtue of how biological organisms explore their environments, in fundamentally new ways and with new combinations, their phase spaces will always continue to grow in size.
We can't know how these phase spaces will change in advance, and as a result, we could never write them down in the form of a law.
Determinists often interject at this point and say, ah yes, but it's still possible to know how these phase spaces change in principle. Really, that's just another way of saying "if we were God." That is, if we could track the positions and momenta of every particle in the universe, we could know how organisms evolve with absolute certainty.
This is a very strange premise to me, since we could never get access to knowledge like that. If you want to disagree with me, and have a design for a supercomputer oracle, please do leave a comment with details.
But as far as I'm aware, something like that would be genuinely impossible. Not to mention the problems that quantum mechanics and Heisenberg's uncertainty principle raises on knowing the positions and momenta of every particle in the observable universe with certainty.
Even Laplace who hypothesized an all-knowing intellect like this, admitted that we would forever be 'infinitely removed' from any kind of knowledge like that.
Contributors to Wikimedia projects
And if laws of biology only exist for God or Laplace's demon and not for us humans, then they don't really exist at all.
Not even the laws of physics predict the evolution of systems perfectly - they're still imperfect idealisations.
For instance, Newton's laws of motion can easily predict how a simple system containing just a ball behaves. But it can't speak for what happens outside this system. I could quite simply intervene to catch the ball and throw it somewhere else.
You have to assume that that doesn't happen for the ball to "obey" Newton's laws.
And if you expand the model to include the forces I impose on the ball, then you run into the same infinite regress from before. Some other factor could always come in and do something to the ball that wasn't in your model.
Newtonian mechanics only models a system accurately if that system is isolated, and if you assume that it remains isolated. Again, this doesn't change in quantum mechanics or general relativity either.
Lee Smolin calls all of these theories doing "physics in a box" since they're most successful when applied to small isolated systems of the universe.
Philosophers on the other hand call these extra assumptions that allow us to draw a box around systems "ceteris-paribus" clauses or "all else being equal" clauses.
But as we've seen in the case of biology, isolated systems don't usually stay isolated. All else does not usually remain equal. Especially outside of nicely constrained laboratory conditions.
So if there are no laws of biology, in the sense of universal differential equations, then what is that theoretical biologists are looking for?
Well, that much is actually quite clear. Theoretical biologists construct models of biology that help us to better understand life. None of them are perfect, and they all require idealisations, abstractions and misrepresentations of reality. But each brings a useful perspective to the table, helping us to understand life's complexity, once we look at many different models together.
We'll never get to a theory of everything because this process doesn't have an endpoint. Scientists can only generate knowledge about the world that gets revised, debated, thrown out, improved, questioned and is forever going to be changing.
Not to mention that the biosphere itself evolves over time through its ever-expanding configuration spaces.
So science has to therefore be a perspectival process, not an immutable bank of universal laws.
I'll finish with a quote from Michela Massimi's book Perspectival Realism:
If ever there was anything miraculous about the success of science, it is not the success of an individual scientific theory … latching onto a mind-independent world. It is the success of our human species in building over time an extraordinarily varied and reliable knowledge of the world we live in, despite having no privileged standpoint to occupy.
Michela MassimiCredits
Member discussion: